用Numpy拆解神经网络

深度学习的核心是神经网络，通过了解其内部计算方法，可以帮助大家更好地理解整个深度学习模型的原理和基本概念，如前向传播、反向传播、激活函数、损失函数等。从本期开始，在介绍高光谱的同时，将同步穿插介绍一些关于深度学习的知识，本篇主要介绍如何用Numpy复现一个简单的神经网络，并构建一个在线识别手写数字的应用。

神经网络计算过程
Numy构建多层感知机
网络训练和测试
在线手写数字识别app

参考资料： - http://f6a.cn/NxPKp - http://f6a.cn/WedtT

（1）网络的前向传播过程：

以下是一个三层的神经网络，假设输入数据为 X，隐藏层的输出为 a1，输出层的输出为 a2，权重矩阵为 W1 和 W2，偏置向量为 b1 和 b2，使用 sigmoid 激活函数。 \[ z1 = X * W1 + b1 \] $$

a1 = sigmoid(z1)

\[ \] z2 = a1 * W2 + b2 \[ \] a2 = sigmoid(z2) $$

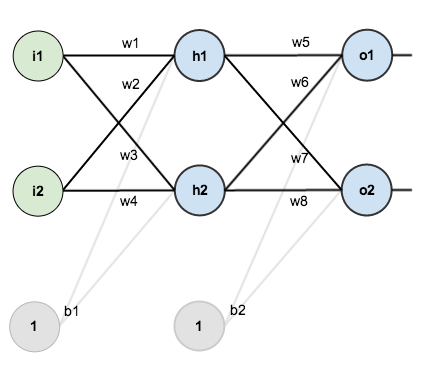
（2）网络的反向传播过程：

假设损失函数为 L，隐藏层的输出为 a1，输出层的输出为 a2，隐藏层的输入为 z1，输出层的输入为 z2，学习率为 lr。

首先，计算输出层的梯度： \[ \frac{\partial L}{\partial a_2} = \frac{\partial L}{\partial a_2} \odot \sigma'(z_2) \]

然后，计算隐藏层的梯度： \[ \frac{\partial L}{\partial a_1} = (\frac{\partial L}{\partial a_2} \cdot W_2^\top) \odot \sigma'(z_1) \]

接下来，计算权重和偏置的梯度，以W1和b1为例，W2和b2计算方式相同： \[ \frac{\partial L}{\partial W_1} = X^\top \cdot \frac{\partial L}{\partial a_1} \\ \frac{\partial L}{\partial b_1} = \sum{\frac{\partial L}{\partial a_1}} \]

最后，使用梯度下降法更新权重和偏置，仅以W1为例，其他三个参数的更新方式相同： \[ W_1 = W_1 - \text{lr} \cdot \frac{\partial L}{\partial W_1} \\ \]

这里使用的是链式法则来计算梯度，从输出层开始，逐层向前反向传播梯度。然后，使用梯度下降法根据学习率 lr 来更新权重和偏置。

1. 基于Numpy构建神经网络

import numpy as np
from tensorflow.keras.datasets import mnist
from matplotlib import pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def Dsigmoid(x):
    return sigmoid(x)*(1-sigmoid(x))

class NN(object):
    def __init__(self, k_in, k_h, k_out, batch_size, lr):
        self.lr = lr                                        # learning rate
        self.W1 = np.random.randn(k_in, k_h) * 0.01          # 输入层到隐藏层的权重矩阵
        self.b1 = np.random.randn(k_h) * 0.01                # 隐藏层的偏置向量
        self.W2 = np.random.randn(k_h, k_out) * 0.01         # 隐藏层到输出层的权重矩阵
        self.b2 = np.random.randn(k_out) * 0.01              # 输出层的偏置向量
        self.bs = batch_size                                 # 批量大小
        print(self.W1.shape, self.b1.shape, self.W2.shape, self.b2.shape)
    
    # 前向传播
    def predict(self,X):
        self.X = X                                           # 输入数据
        self.z1 = np.dot(X, self.W1) + self.b1                # 隐藏层输入
        self.a1 = sigmoid(self.z1)                            # 隐藏层激活输出
        self.z2 = np.dot(self.a1, self.W2) + self.b2          # 输出层输入
        self.a2 = sigmoid(self.z2)  
        return self.a2                                       # 输出层激活输出      
    
    def forward(self, X, y):
        self.X = X                                           # 输入数据
        self.a2 = self.predict(self.X)                            # 输出层激活输出
        loss = np.sum((self.a2 - y) * (self.a2 - y)) / 2      # 计算损失（均方差）
        self.d2 = (self.a2 - y) * Dsigmoid(self.z2)           # 输出层的误差
        return loss, self.a2

    # 反向传播
    def backward(self):
        dW2 = np.dot(self.a1.T, self.d2) / self.bs                  # 隐藏层到输出层的权重梯度
        db2 = np.sum(self.d2, axis=0) / self.bs                     # 输出层偏置的梯度
        d1 = np.dot(self.d2, self.W2.T) * Dsigmoid(self.z1)         # 隐藏层的误差
        dW1 = np.dot(self.X.T, d1) / self.bs                        # 输入层到隐藏层的权重梯度
        db1 = np.sum(d1, axis=0) / self.bs                          # 隐藏层偏置的梯度

        self.W2 -= self.lr * dW2             # 更新隐藏层到输出层的权重
        self.b2 -= self.lr * db2             # 更新输出层的偏置
        self.W1 -= self.lr * dW1             # 更新输入层到隐藏层的权重
        self.b1 -= self.lr * db1             # 更新隐藏层的偏置

2. 手写字体数字在线识别应用

2.1 数据处理

(X_train, Y_train), (X_valid, Y_valid) = mnist.load_data()
print(X_train.shape,Y_train.shape,X_valid.shape,Y_valid.shape)

(60000, 28, 28) (60000,) (10000, 28, 28) (10000,)

fig=plt.figure(figsize=(25,5))
for i in range(10):
    plt.subplot(1,10,i+1)
    plt.axis('off')
    plt.imshow(X_train[i,:,:])
fig.tight_layout()
plt.show()

def onehot(targets, num):
    result = np.zeros((num, 10))
    for i in range(num):
        result[i][targets[i]] = 1
    return result

X_train=X_train.reshape(60000, 28*28) / 255. 
X_valid=X_valid.reshape(10000, 28*28) / 255. 
y_train = onehot(Y_train, 60000) # (60000, 10)
y_valid = onehot(Y_valid, 10000) # (10000, 10)
print(X_train.shape,y_train.shape,X_valid.shape,Y_valid.shape)
print(np.max(X_train),np.max(X_valid))

(60000, 784) (60000, 10) (10000, 784) (10000,)
1.0 1.0

2.2 训练模型

def calculate_accuracy(y_true, y_pred):
    y_true_labels = np.argmax(y_true, axis=1)
    y_pred_labels = np.argmax(y_pred, axis=1)
    correct_predictions = np.sum(y_true_labels == y_pred_labels)
    accuracy = correct_predictions / len(y_true)
    return accuracy

def train(k_in, k_h, k_out, batch_size, lr, epochs):
    nn = NN(k_in, k_h, k_out, batch_size, lr)     # 创建神经网络对象  
    log = {'train_loss': [], 'train_acc': []} # 存储训练过程的损失和准确率
    
    # 开始训练循环
    for epoch in range(epochs):
        epoch_train_loss = 0.0
        epoch_train_correct = 0

        # 分批次训练
        for i in range(0, X_train.shape[0], batch_size):
            X = X_train[i:i + batch_size] # 获取当前批次的训练数据
            y = y_train[i:i + batch_size] # 获取当前批次的标签
            loss, y_pred = nn.forward(X, y) # 前向传播计算损失并获取预测结果
            nn.backward()  # 反向传播更新参数
            epoch_train_loss += loss # 累计当前批次内的损失率
            epoch_train_correct += calculate_accuracy(y, y_pred) # 累计当前批次内和准确率

        # 计算单个轮次内的平均损失和准确率
        train_loss = epoch_train_loss / (X_train.shape[0] // batch_size)
        train_acc = epoch_train_correct / (X_train.shape[0] // batch_size)

        # 将训练过程的损失和准确率记录到日志中
        log['train_loss'].append(train_loss)
        log['train_acc'].append(train_acc)

        print("Epoch:", epoch, "...................", "Loss： {:.3f}   Acc: {:.3f}".format(train_loss, train_acc))
    
    np.savez("./nnmodel.npz", w1=nn.W1, b1=nn.b1, w2=nn.W2, b2=nn.b2) # 保存训练后的参数
    
    # 返回训练过程的损失和准确率
    return log

k_in=X_train.shape[1]
k_h=100
k_out=len(np.unique(Y_valid))
batch_size=50
epochs=30
lr=0.5
log=train(k_in,k_h,k_out,batch_size,lr,epochs)

(784, 100) (100,) (100, 10) (10,)
Epoch: 0 ................... Loss： 16.001   Acc: 0.501
Epoch: 1 ................... Loss： 6.050   Acc: 0.880
Epoch: 2 ................... Loss： 4.432   Acc: 0.905
Epoch: 3 ................... Loss： 3.831   Acc: 0.915
Epoch: 4 ................... Loss： 3.466   Acc: 0.922
Epoch: 5 ................... Loss： 3.201   Acc: 0.928
......................................

def plot_log(log):
    plt.style.use("ggplot")
    fig, axs = plt.subplots(1, 2, figsize=(10, 4))
    axs[0].plot(log['train_loss'], '#008000')
    axs[0].set_title('Training Loss')
    axs[0].set_xlabel('Epochs')
    axs[0].set_ylabel('Loss')
    axs[1].plot(log['train_acc'], '#008000')
    axs[1].set_title('Training Accuracy')
    axs[1].set_xlabel('Epochs')
    axs[1].set_ylabel('Accuracy')
    plt.tight_layout()  
    plt.show()
plot_log(log)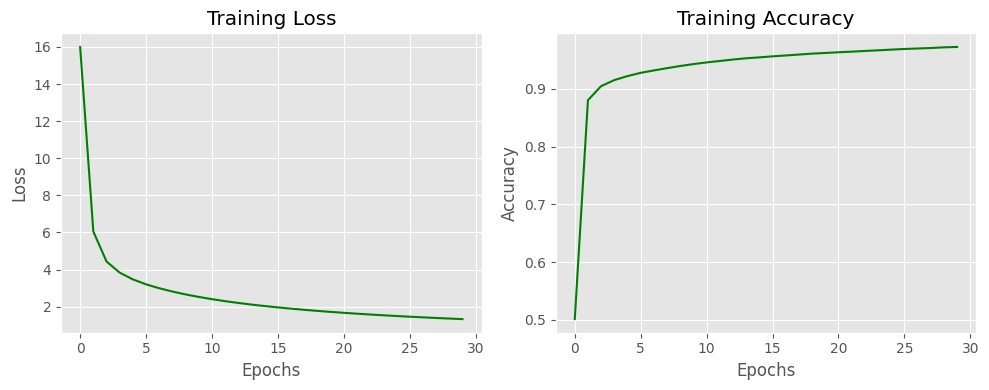

2.3 测试模型

def load_model(k_in,k_h,k_out,batch_size,lr):
    r = np.load("./nnmodel.npz")
    nn = NN(k_in,k_h,k_out,batch_size,lr)
    nn.W1 = r["w1"]
    nn.b1 = r["b1"]
    nn.W2 = r["w2"]
    nn.b2 = r["b2"]
    return nn

model=load_model(k_in,k_h,k_out,batch_size,lr)
val_pred = model.predict(X_valid)
val_acc=calculate_accuracy(y_valid,val_pred)
print("Val Precison:", val_acc)

(784, 100) (100,) (100, 10) (10,)
Val Precison: 0.9658

fig = plt.figure(figsize=(10, 5))
for i in range(8):
    plt.subplot(2, 4, i+1)
    plt.axis('off')
    plt.imshow(X_valid.reshape(10000, 28, 28)[i+20, :, :],cmap='gray')
    plt.title("Pred:    {}".format(int(np.argmax(model.predict(X_valid)[i+20]))))
fig.tight_layout()
plt.show()

2.4 构建交互app

import gradio as gr
# 构建预测函数
def predict_minist(image):
    normalized = np.array(image)/ 255.0
    # np.save("image.npy", normalized)
    flattened = normalized.reshape(1, 784)
    prediction = model.predict(flattened)
    pred_index = int(np.argmax(prediction,axis=-1))
    return pred_index

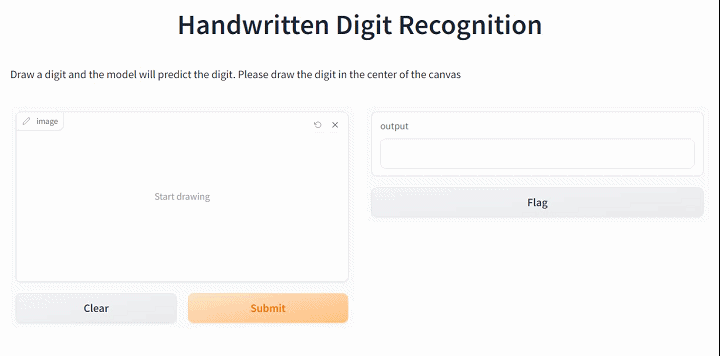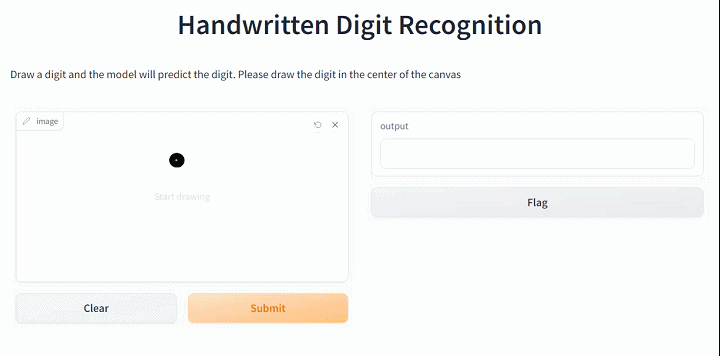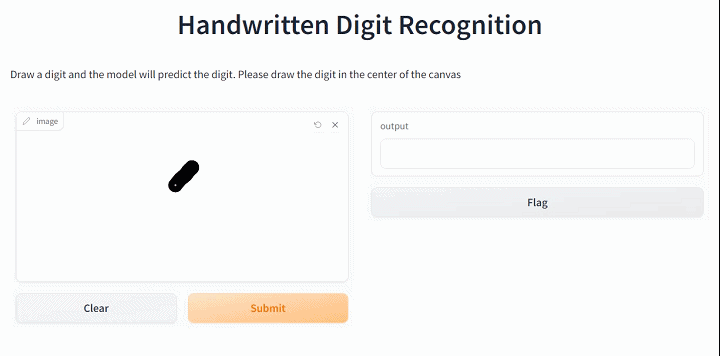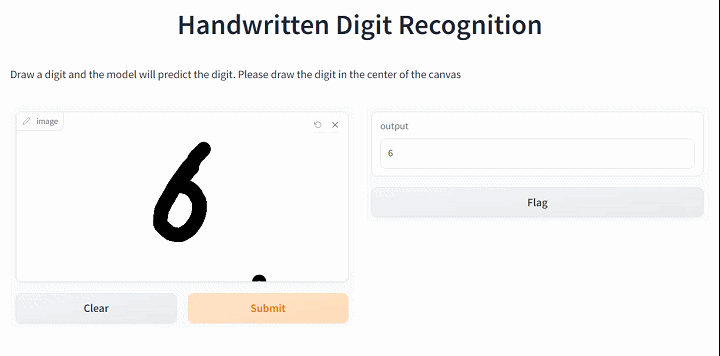
iface = gr.Interface(fn=predict_minist, inputs=gr.Sketchpad(), outputs="text",
                     title="Handwritten Digit Recognition",
                     description="Draw a digit and the model will predict the digit. Please draw the digit in the center of the canvas")

iface.launch(height=550,width="100%",show_api=False)

Running on local URL:  http://127.0.0.1:7888

To create a public link, set `share=True` in `launch()`.

请关注微信公众号【45度科研人】获取更多精彩内容，欢迎后台留言！